Single-Nucleon Momentum Distributions

Two-Nucleon Momentum Distributions

This web page presents single-nucleon momentum distributions calculated for a variety of nuclei in the range A=2-12. Corresponding two-nucleon momentum distributions can be found here. These are from variational Monte Carlo calculations (VMC) using either the Argonne v18 two-nucleon and Urbana X three-nucleon potentials (AV18+UX) or one of the Norfolk Δ-full chiral effective field theory interactions: NV2+3-Ia, -Ia*, -Ib*, -IIa*, -IIb*.

Original density and momentum distribution results for AV18+UX were reported in:
Wiringa, et al., Phys. Rev. C 89, 024305 (2014).

The results with Norfolk chiral EFT interactions are reported in:
Piarulli, et al., Phys. Rev C 107, 014314 (2023).

Please cite the above papers when using results from these pages.

These VMC wave functions are the starting trial functions for a number of recent Green's function Monte Carlo (GFMC) calculations:
Brida, et al., Phys. Rev. C 84, 024319 (2011);
McCutchan, et al., Phys. Rev. C 86, 024315 (2012);
Pastore, et al., Phys. Rev. C 87, 035503 (2013);
Datar, et al., Phys. Rev. Lett. 111, 062502 (2013);
Pastore, et al., Phys. Rev. C 90, 024321 (2014).

More details of the wave function construction can be found in
Wiringa, Phys. Rev. C 43, 1585 (1991) for A=3,4;
Pudliner, et al., Phys. Rev. C 56, 1720 (1997) for A=6,7;
Wiringa, et al., Phys. Rev. C 62, 014001 (2000) for A=8;
Pieper, et al., Phys. Rev. C 70, 044310 (2002) for A=9,10.

An excellent overall review of quantum Monte Carlo methods for nuclei can be found at:
Carlson, et al., Rev. Mod. Phys. 87, 1067 (2015)

The largest nuclei are evaluated using the cluster VMC (CVMC) method.

The CVMC method is described in
Pieper, et al., Phys. Rev. C 46, 1741 (1992) for A=16 with AV1 4+UVII
Lonardoni, et al., Phys. Rev. C 96, 024326 (2017) for A=16,40 with AV18+UIX.

The Norfolk interactions are described and used in the following papers:
Piarulli, et al., Phys. Rev. C 94, 054007 (2016).
Piarulli, et al., Phys. Rev. Lett. 120, 052503 (2018).
Baroni, et al., Phys. Rev. C 98, 044003 (2018).
Schiavilla, et al., Phys. Rev. C 99, 034005 (2019).

Momentum distributions are provided for neutron spin-down, neutron spin-up, proton spin-down, and proton spin-up cases, for the M=J state. The single-nucleon densities corresponding to these wave functions are given here

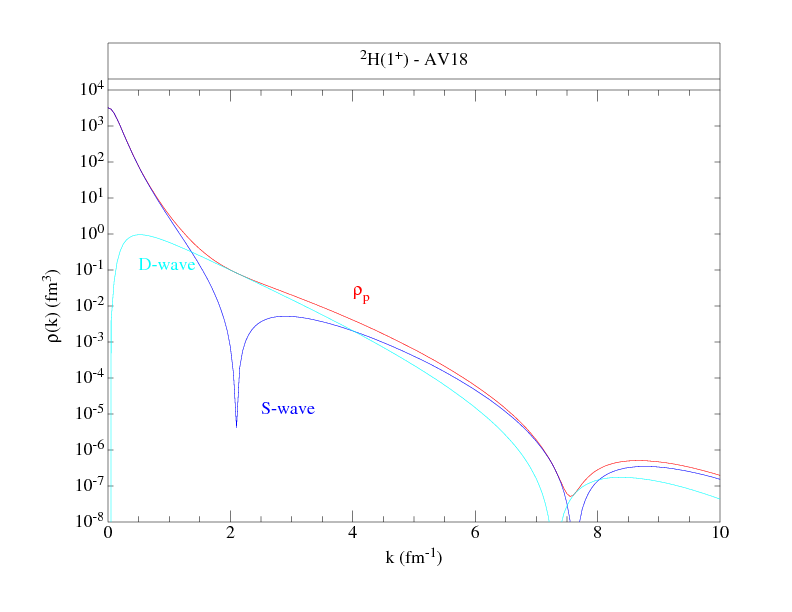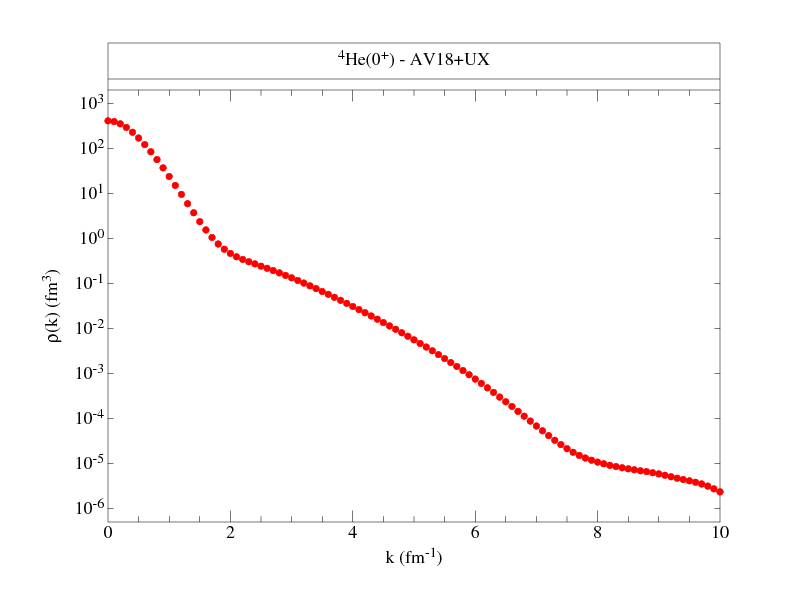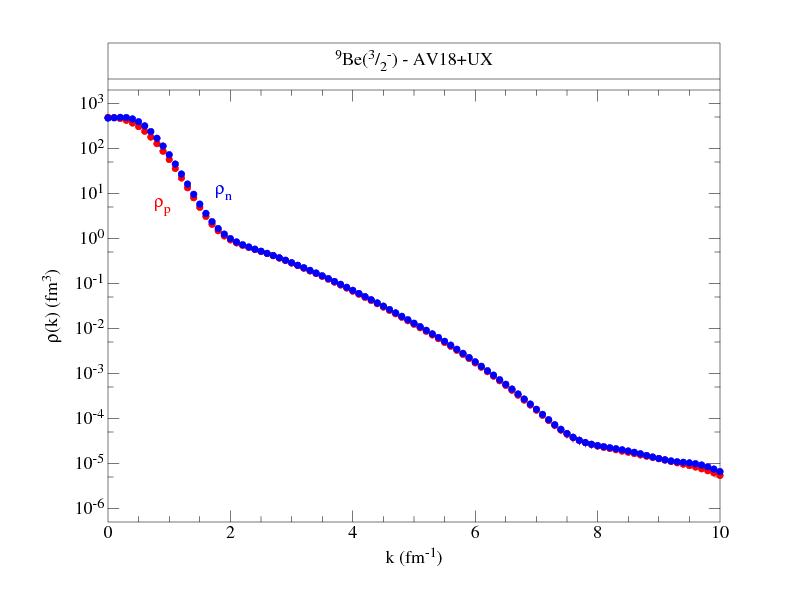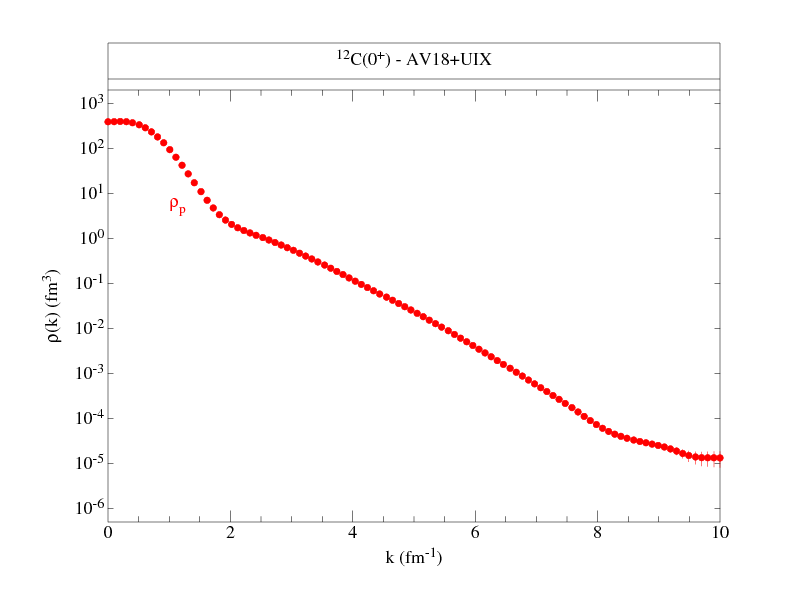
Following are files that tabulate the proton and neutron momentum distributions along with figures to give an overall view of the distributions. The normalization is chosen such that:

ANS = 1/(2π)3 ∫ d3k ρNS(k)

where NS denotes proton or neutron, spin up or down, and ANS is the total number (out of A) nucleons with the given nucleon-spin projection. Where proton and neutron momentum distributions are the same, as in T=0 nuclei, we give only one set, and similarly, if spin-up and spin-down projections are the same, as in 0+ states, we give totals only. The kinetic energy from these distributions is also given.

2H(1+)
AV18
Figure
Table 		2H(1+)
NV2-Ia
Figure
Table 		2H(1+)
NV2-Ib
Figure
Table 		2H(1+)
NV2-IIa
Figure
Table 		2H(1+)
NV2-IIb
Figure
Table
3H(1/2+)
AV18+UX
Figure 1
Figure 2
Figure 3
Table
Table (dn) 		3H(1/2+)
NV2+3-Ia
Figure 1
Figure 2
Figure 3
Table
Table (dn) 		3H(1/2+)
NV2+3-Ia*
Figure 1
Figure 2
Table


 3H(1/2+)
NV2+3-Ib*
Figure 1
Figure 2
Table


 3H(1/2+)
NV2+3-IIa*
Figure 1
Figure 2
Table


 3H(1/2+)
NV2+3-IIb*
Figure 1
Figure 2
Table
3He(1/2+)
AV18+UX
Figure 1
Figure 2
Figure 3
Table
Table (dp) 		3He(1/2+)
NV2+3-Ia
Figure 1
Figure 2
Figure 3
Table
Table (dn) 		3He(1/2+)
NV2+3-Ia*
Figure 1
Figure 2
Table


 3He(1/2+)
NV2+3-Ib*
Figure 1
Figure 2
Table


 3He(1/2+)
NV2+3-IIa*
Figure 1
Figure 2
Table


 3He(1/2+)
NV2+3-IIb*
Figure 1
Figure 2
Table
4He(0+)
AV18+UX
Figure 1
Figure 2
Table
Table (tp+dd) 		4He(0+)
AV18+UIX
Figure
Table


 4He(0+)
AV18
Figure
Table


 4He(0+)
NV2+3-Ia
Figure
Figure 2
Table
Table (tp+dd) 		4He(0+)
NV2+3-Ia*
Figure
Table


 4He(0+)
NV2+3-Ib*
Figure
Table


 4He(0+)
NV2+3-IIa*
Figure
Table


 4He(0+)
NV2+3-IIb*
Figure
Table
6He(0+)
AV18+UX
Figure 1
Figure 2
Table 		6He(0+)
NV2+3-Ia
Figure 1
Figure 2
Table
 6He(0+)
NV2+3-Ia*
Figure 1
Figure 2
Table
 6He(0+)
NV2+3-Ib*
Figure 1
Figure 2
Table
 6He(0+)
NV2+3-IIa*
Figure 1
Figure 2
Table
 6He(0+)
NV2+3-IIb*
Figure 1
Figure 2
Table
6Li(1+)
AV18+UX
Figure 1
Figure 2
Figure 3
Table
Table (αd) 		6Li(3+)
AV18+UX
Figure 1
Figure 2
Figure 3
Table
Table (αd) 		6Li(1+)
NV2+3-Ia
Figure 1
Figure 2
Figure 3
Table
Table (αd)
 6Li(1+)
NV2+3-Ia*
Figure 1
Figure 2

Table

 6Li(1+)
NV2+3-Ib*
Figure 1
Figure 2

Table

 6Li(1+)
NV2+3-IIa*
Figure 1
Figure 2

Table

 6Li(1+)
NV2+3-IIb*
Figure 1
Figure 2

Table
7Li(3/2-)
AV18+UX
Figure 1
Figure 2
Figure 3
Table
Table (αt) 		7Li(1/2-)
AV18+UX
Figure 1
Figure 2
Figure 3
Table
Table (αt) 		7Li(7/2-)
AV18+UX
Figure 1
Figure 2
Figure 3
Table
Table (αt) 		7Li(5/2-)
AV18+UX
Figure 1
Figure 2
Figure 3
Table
Table (αt) 		7Li(5/2-)_2
AV18+UX
Figure 1
Figure 2
Figure 3
Table
Table (αt) 		7Li(3/2-)
NV2+3-Ia
Figure 1
Figure 2
Figure 3
Table
Table (αt)
 7Li(3/2-)
NV2+3-Ia*
Figure 1
Figure 2
Table


 7Li(3/2-)
NV2+3-Ib*
Figure 1
Figure 2
Table


 7Li(3/2-)
NV2+3-IIa*
Figure 1
Figure 2
Table


 7Li(3/2-)
NV2+3-IIb*
Figure 1
Figure 2
Table
8He(0+)
AV18+UX
Figure 1
Figure 2
Table 		8He(0+)
NV2+3-Ia
Figure 1
Figure 2
Table
 8He(0+)
NV2+3-Ia*
Figure 1
Figure 2
Table
 8He(0+)
NV2+3-Ib*
Figure 1
Figure 2
Table
 8He(0+)
NV2+3-IIa*
Figure 1
Figure 2
Table
 8He(0+)
NV2+3-IIb*
Figure 1
Figure 2
Table
8Li(2+)
AV18+UX
Figure 1
Figure 2
Figure 3
Table 		8Li(2+)
NV2+3-Ia
Figure 1
Figure 2
Figure 2
Table
 8Li(2+)
NV2+3-Ia*
Figure 1
Figure 2
Figure 2
Table
 8Li(2+)
NV2+3-Ib*
Figure 1
Figure 2
Figure 2
Table
 8Li(2+)
NV2+3-IIa*
Figure 1
Figure 2
Figure 2
Table
 8Li(2+)
NV2+3-IIb*
Figure 1
Figure 2
Figure 2
Table
 8B(2+)
AV18+UX
Figure 1
Figure 2
Figure 3
Table
8Be(0+)
AV18+UX
Figure 1
Figure 2
Table
Table (αα) 		8Be(2+)
AV18+UX
Figure 1
Figure 2
Table
Table (αα) 		8Be(4+)
AV18+UX
Figure 1
Figure 2
Table
Table (αα) 		8Be(0+)
NV2+3-Ia
Figure 1
Figure 2
Table
Table (αα)
 8Be(0+)
NV2+3-Ia*
Figure 1
Figure 2
Table

 8Be(0+)
NV2+3-IIb*
Figure 1
Figure 2
Table
9Li(3/2-)
AV18+UX
Figure 1
Figure 2
Table 		9Li(3/2-)
NV2+3-Ia
Figure 1
Figure 2
Table
 9Li(3/2-)
NV2+3-Ia*
Figure 1
Figure 2
Table
 9Li(3/2-)
NV2+3-IIb*
Figure 1
Figure 2
Table
9Be(3/2-)
AV18+UX
Figure 1
Figure 2
Table 		9Be(3/2-)
NV2+3-Ia
Figure 1
Figure 2
Table
 9Be(3/2-)
NV2+3-Ia*
Figure 1
Figure 2
Table
 9Be(3/2-)
NV2+3-Ib*
Figure 1
Figure 2
Table
 9Be(3/2-)
NV2+3-IIa*
Figure 1
Figure 2
Table
 9Be(3/2-)
NV2+3-IIb*
Figure 1
Figure 2
Table
10He(0+)
AV18+UX
Figure 1
Figure 2
Table 		10Be(0+)
AV18+UX
Figure 1
Figure 2
Table 		10Be(0+)
NV2+3-Ia*
Figure 1
Figure 2
Table 		10Be(0+)
NV2+3-IIb*
Figure 1
Figure 2
Table 		10B(3+)
AV18+UX
Figure 1
Figure 2
Table 		10B(3+)
NV2+3-Ia
Figure 1
Figure 2
Table 		10B(3+)
NV2+3-Ia*
Figure 1
Figure 2
Table 		10B(3+)
NV2+3-IIb*
Figure 1
Figure 2
Table
11Li(3/2-)
AV18+UX
Figure 1
Figure 2
Table 		11B(3/2-)
AV18+UX
Figure 1
Figure 2
Table 		11B(3/2-)
NV2+3-Ia*
Figure 1
Figure 2
Table 		11B(3/2-)
NV2+3-IIb*
Figure 1
Figure 2
Table
12Be(0+)
AV18+UX
Figure 1
Figure 2
Table 		12C(0+)
AV18+UX
Figure
Table
12C(0+)
AV18+UIX
Figure
Table
12C(0+)
NV2+3-Ia*
Figure
Table
12C(0+)
NV2+3-IIb*
Figure
Table
16O(0+)
CVMC
AV18
Figure
Table 		16O(0+)
CVMC
AV18+UIX
Figure
Table
40Ca(0+)
CVMC
AV18
Figure
Table 		40Ca(0+)
CVMC
AV18+UIX
Figure
Table

Robert B. Wiringa
Last updated July 26, 2024